Get out from smog – part IV

As i mentioned in a previous post. I create a class that will be calculated the distance in kilometers between the measuring stations and a latitudes, longitudes. First we have to calculate distance in kilometers between latidute and longtidute points.

Haversine formula

In this example, I use Haversine formula to calculate distance.

I wrote it in delegate Func which has four parameters and return ‘double’ as a result.

Func<double, double, double, double, double> calculateDistanceToKm = (double _stationLatitudes 
                    , double _stationLongtitudes, double _userLatitudes, double _userLongtitudes ) =>
    {
        var R = 6372.8; // In kilometers
        var dLat = toRadians(_stationLatitudes - _userLatitudes);
        var dLon = toRadians(_stationLongtitudes - _userLongtitudes);
        _userLatitudes = toRadians(_userLatitudes);
        _stationLatitudes = toRadians(_stationLatitudes);

        var a = Math.Sin(dLat / 2) * Math.Sin(dLat / 2) + Math.Sin(dLon / 2) * Math.Sin(dLon / 2) 
                * Math.Cos(_stationLatitudes) * Math.Cos(_userLatitudes);
        var c = 2 * Math.Asin(Math.Sqrt(a));
        return Math.Round(R * 2 * Math.Asin(Math.Sqrt(a)),3);
    };

Next I filters my list to receive only stations that are up away max. 100km and added properties which defines the distance from the station.

The whole class looks like this:

public class ReturnNearestStationsIn100Km: IReturnNearestStation
{
    public List<ParseJsonToList> ReturnNearestStation(List<ParseJsonToList> model, double userLatitudes, double userLongitudes)
    {
        Func<double, double, double, double, double> calculateDistanceToKm = (double _stationLatitudes, double _stationLongtitudes, double _userLatitudes, double _userLongtitudes) =>
            {
                var R = 6372.8; // In kilometers
                var dLat = toRadians(_stationLatitudes - _userLatitudes);
                var dLon = toRadians(_stationLongtitudes - _userLongtitudes);
                _userLatitudes = toRadians(_userLatitudes);
                _stationLatitudes = toRadians(_stationLatitudes);

                var a = Math.Sin(dLat / 2) * Math.Sin(dLat / 2) + Math.Sin(dLon / 2) * Math.Sin(dLon / 2) * Math.Cos(_stationLatitudes) * Math.Cos(_userLatitudes);
                var c = 2 * Math.Asin(Math.Sqrt(a));
                return Math.Round(R * 2 * Math.Asin(Math.Sqrt(a)), 3);
            };
        var filtredModel = model.Where(x =>
        {
            var distanceInKmFromUserToStation = calculateDistanceToKm(x.LatAndLong.Latitudes, x.LatAndLong.Longitudes, userLatitudes, userLongitudes);
            x.DistanceBetweenUserAndStation = distanceInKmFromUserToStation;
            return (distanceInKmFromUserToStation < 100);
        }).ToList();
        return filtredModel;
    }
    public double toRadians(double angle)
    {
        return Math.PI * angle / 180.0;
    }
}

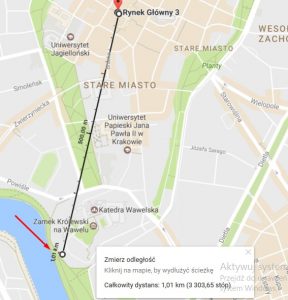
And here is test for check the distance between the Main Market Square in Krakow and the Wawel Dragon which is ~1012 meters.

Test class:

public class CalculateDistanceBetweenLatiduteAndLongitudeTest
{
    [Fact]
    public void Distance_between_main_market_square_and_wawel_dragon_should_be_1km_and_12meters()
    {
        double _mainMarketSquareCracovLatitude = 50.061858;
        double _mainMarketSquareCracovlongtitude = 19.936833;
        double _wawelDragonLatitude = 50.053001;
        double _wawelDragonLongtitude = 19.933568;
        List<ParseJsonToList> model = new List<ParseJsonToList>();
        LatitudesLongitudes testLatAndLong = new LatitudesLongitudes();
        testLatAndLong.Latitudes = _mainMarketSquareCracovLatitude;
        testLatAndLong.Longitudes = _mainMarketSquareCracovlongtitude;
        model.Add(new ParseJsonToList()
        {
            LatAndLong = testLatAndLong
        });

        ReturnNearestStationsIn100Km calc = new ReturnNearestStationsIn100Km();

        var result = calc.ReturnNearestStation(model, _wawelDragonLatitude, _wawelDragonLongtitude);

        Assert.Equal(1.012d, result.FirstOrDefault().DistanceBetweenUserAndStation);
    }
}

Distance from google maps.

Summary

The next step will be combining all written so far functionality and display the nearest station’s.

Link to the project: HERE.